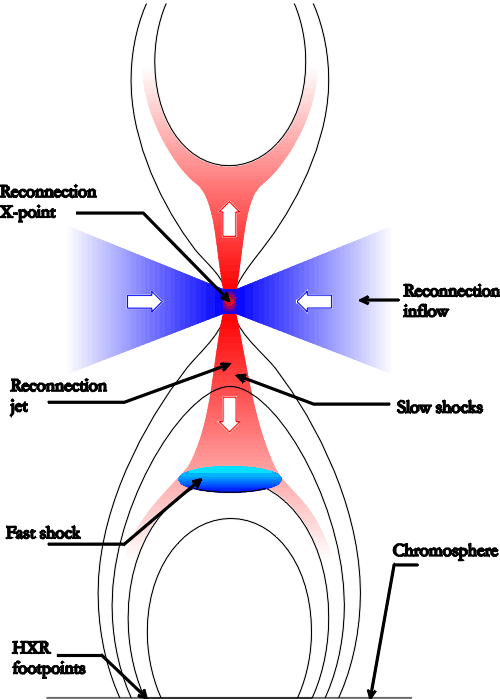
| Class | Intensity (erg cm-2 s-1) |
| B | 10-4 |
| C | 10-3 |
| M | 10-2 |
| X | 10-1 |
| (2.1) |

| (2.2) |
| (2.3) |
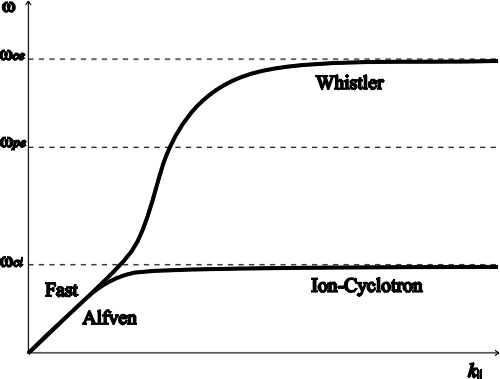
| (2.4) |
| (2.5) |
| (2.6) |
| (2.7) |
| (2.8) |
| (2.9) |
| (2.10) |
| (2.11) |
| (2.12) |
| (2.13) |
| (2.14) |
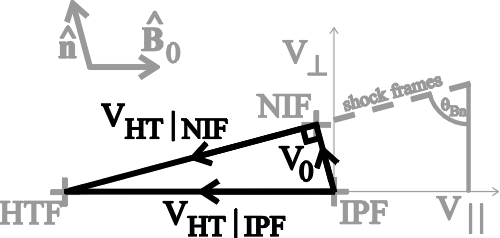
| (2.15) |
| (2.16) |
| (2.17) |
| (2.18) |
| (2.19) |
| (2.20) |
| (2.21) |
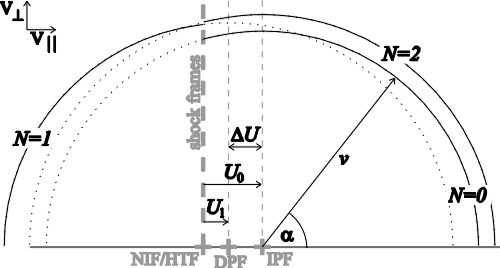
| (2.22) |
| (2.23) |
| (2.24) |
| (2.25) |
| (2.26) |
| (2.27) |
| (2.28) |
| (2.29) |
| (2.30) |
| (2.31) |
| (2.32) |
| (2.33) |
| (2.34) |
| (2.35) |
| (2.36) |
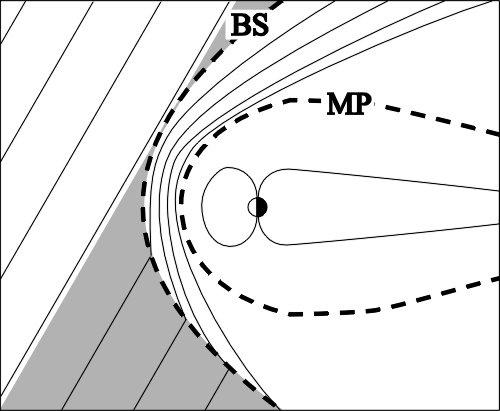
| Parameter | Flare shock | Bow shock |
| MA | 1.0-1.6 | 4-10 |
| qBn | unknown | depends on position |
| Rc | unknown | � 15 RE |
| vA | 160 km s-1 | 40 km s-1 |
| vA Wi-1 | 10 m | 80 km |
| b | 0.01 - 0.1 | 1.6 |
| B | 130 - 190 mT | 7 nT |
| Te | 300 eV | 10 - 60 eV |
| (2.37) |