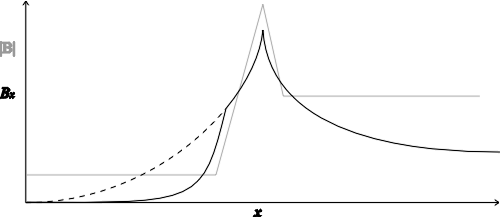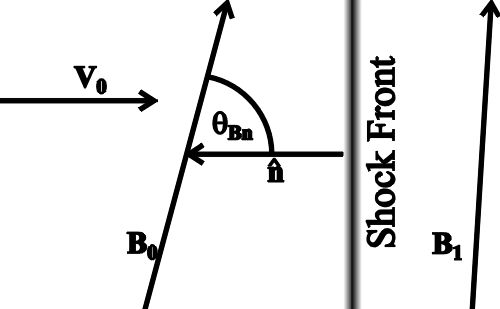

| Parameter | Symbol | Value |
| cell size in x | Dx | 0.2 vA Wi-1 |
| cell size in y | Dy | 0.2 vA Wi-1 |
| time step | Dt | 0.01 Wi-1 |
| number of cells in x | nx | 360 |
| number of cells in y | ny | 128 |
| number of time steps | nt | 4000 |
| electron plasma beta | be | 0.5 |
| perpendicular ion temperature | Ti^ | 0.5 |
| parallel ion temperature | Ti|| | 0.5 |
| number of field substeps | ns | 10 |
| number of ions per cell | 50 |
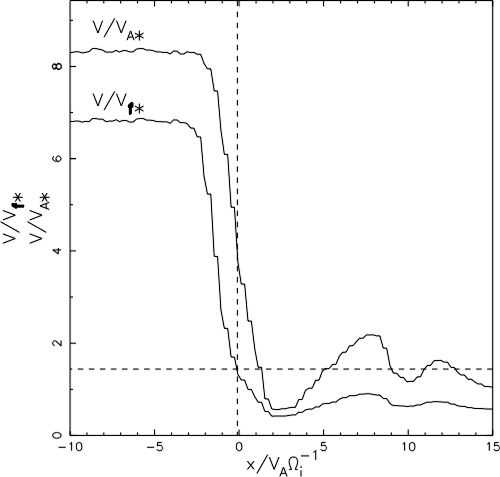
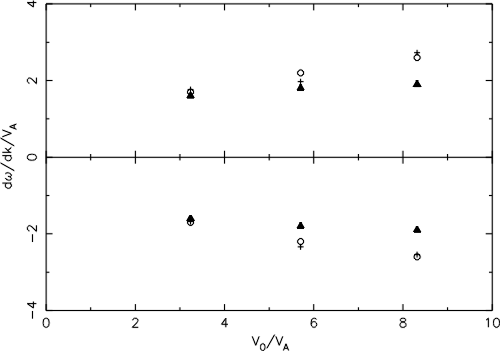
| Plasma inflow speed in | shock Alfvén Mach number, MA | |
| simulation frame, Vin | qBn =85� | qBn =88� |
| 2 vA | 3.32 | 3.33 |
| 4 vA | 5.66 | 5.66 |
| 6 vA | 8.29 | 8.21 |
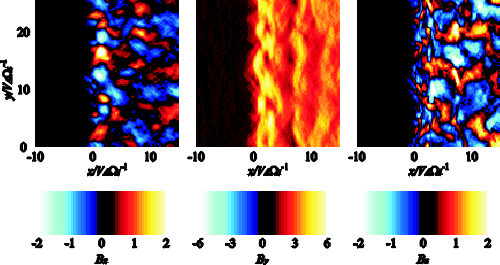
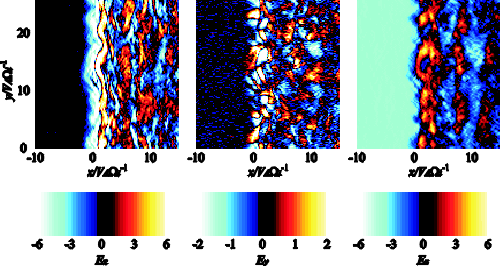
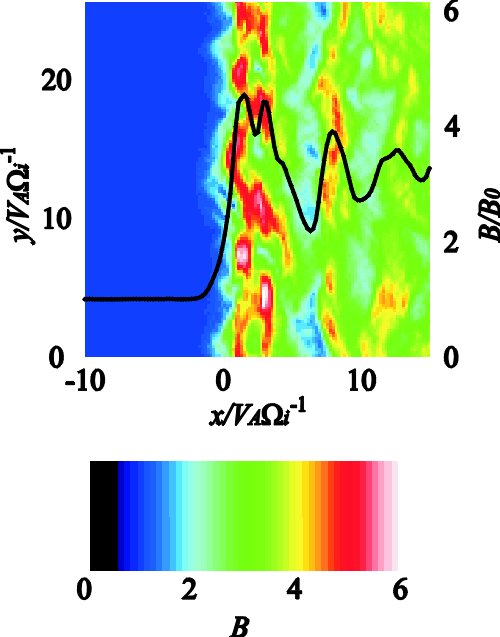
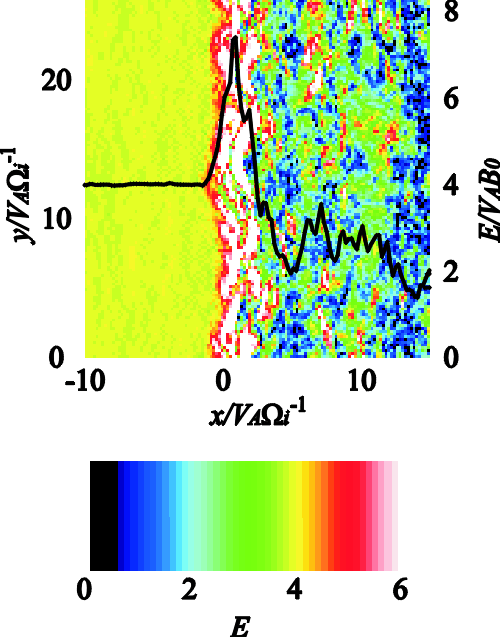
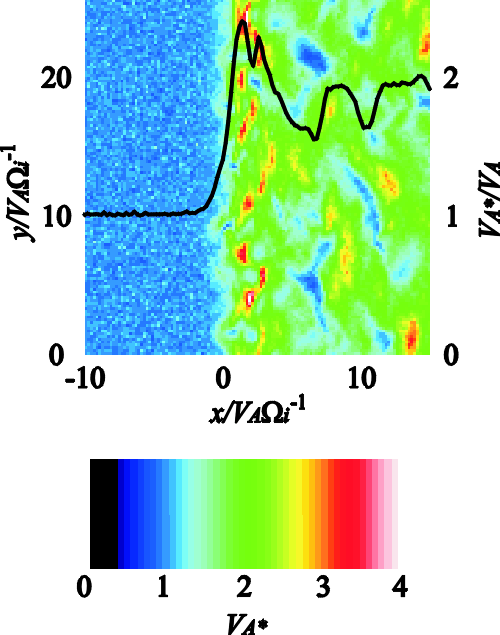
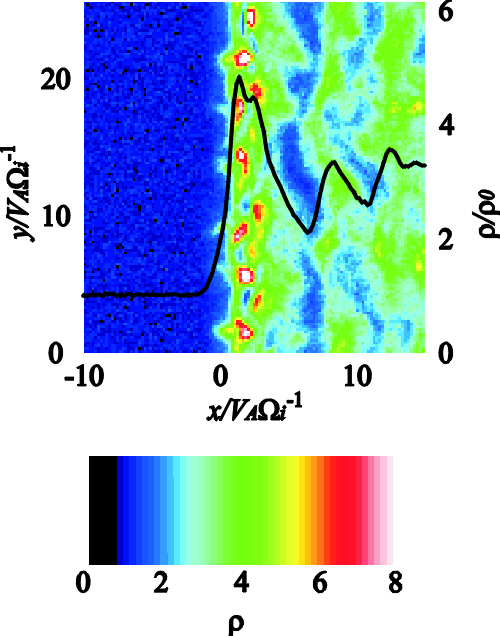
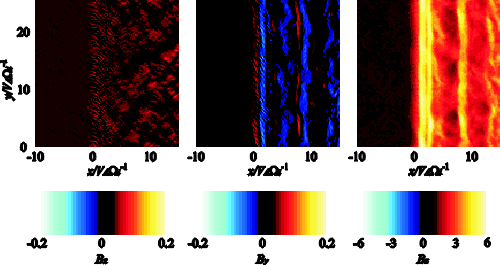
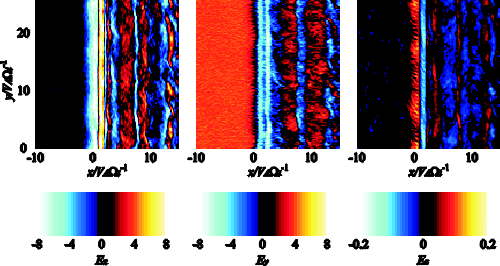
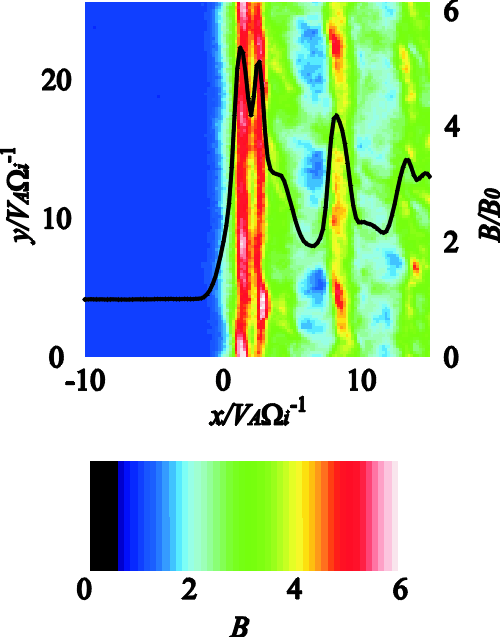
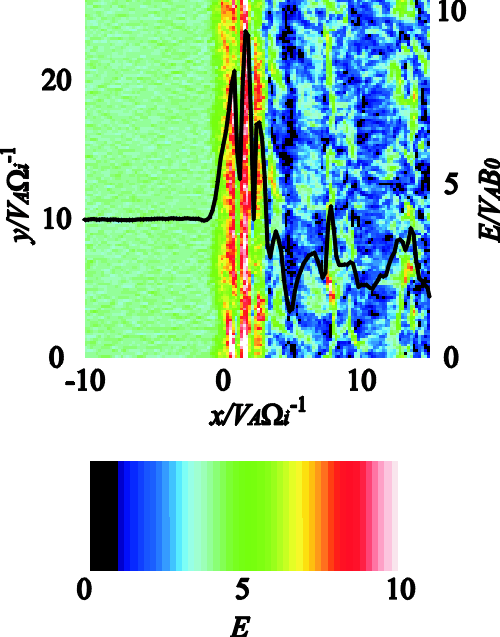
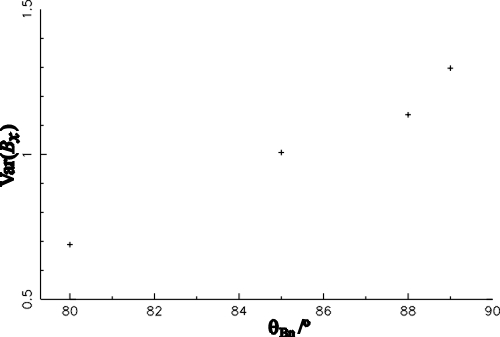
| (4.1) |
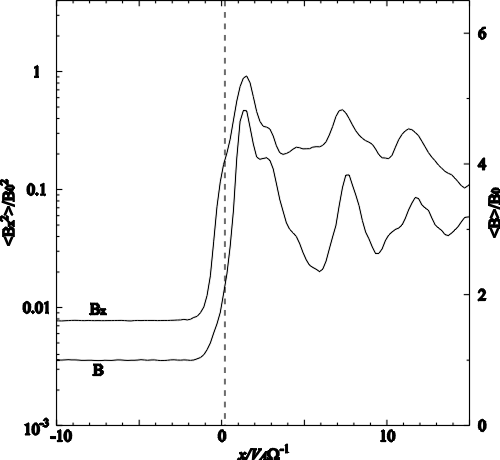
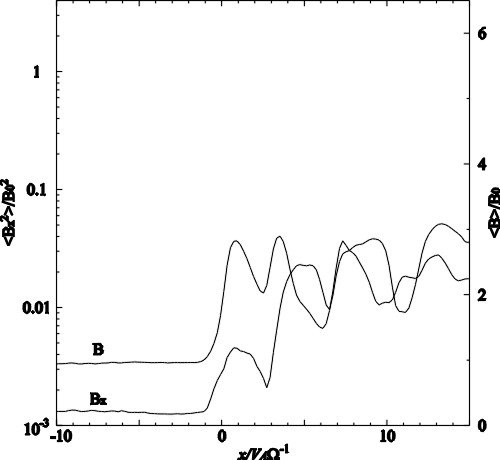
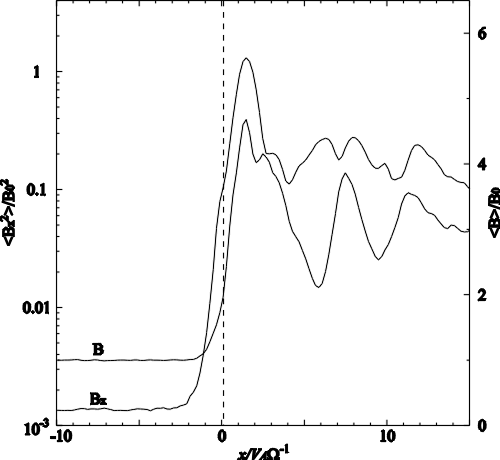
| (4.2) |
| (4.3) |
| (4.4) |
| (4.5) |
| (4.6) |
| (4.7) |
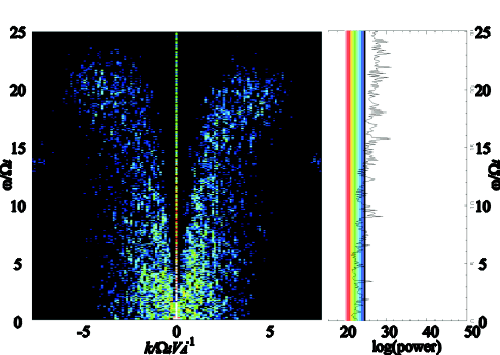
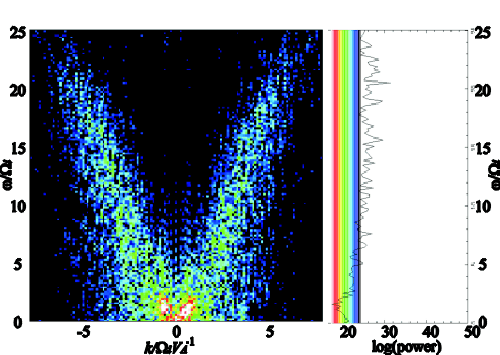
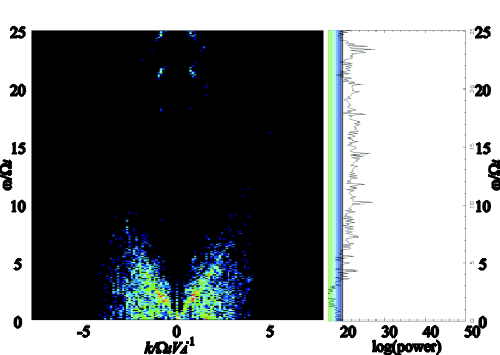
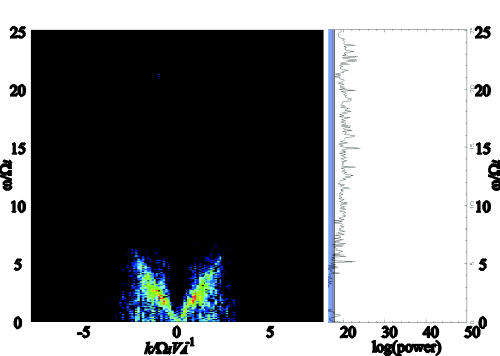
| Plasma inflow speed | [(�w)/(�k)] | |
| Vin | - branch | + branch |
| 2 vA | -1.68 vA | 1.76 vA |
| 4 vA | -2.34 vA | 1.97 vA |
| 6 vA | -2.54 vA | 2.73 vA |
| (4.8) |
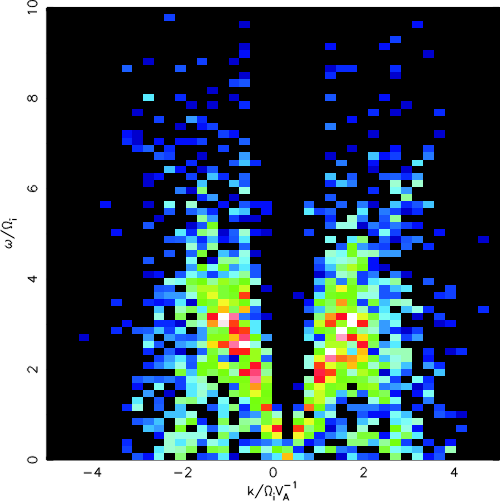
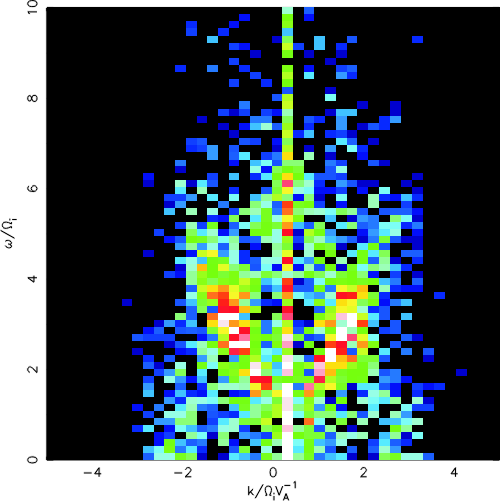
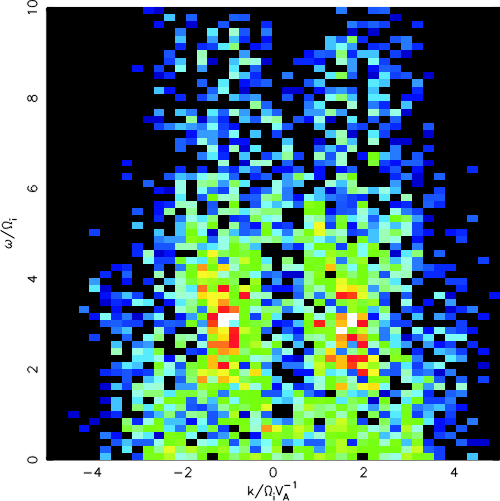
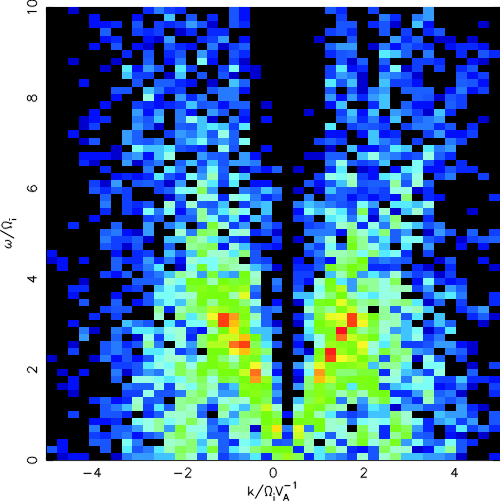
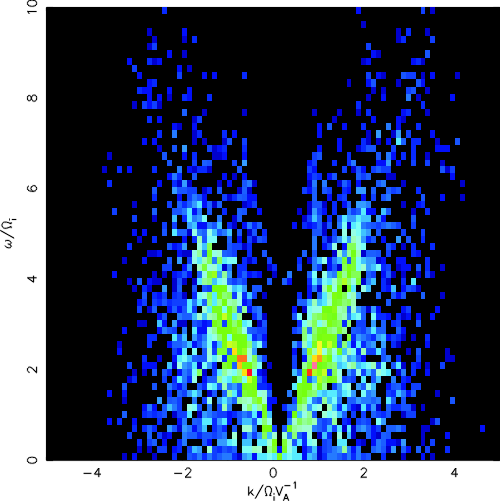
| Dx | Dy | Dt | [(�w)/(�k)] | |
| - branch | + branch | |||
| 0.2 vA Wi-1 | 0.2 vA Wi-1 | 0.01 Wi-1 | -2.21 vA | 2.19 vA |
| 0.4 vA Wi-1 | 0.4 vA Wi-1 | 0.02 Wi-1 | -2.40 vA | 2.34 vA |