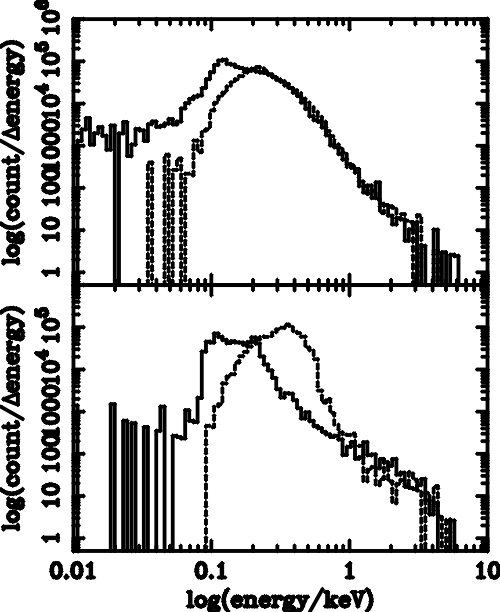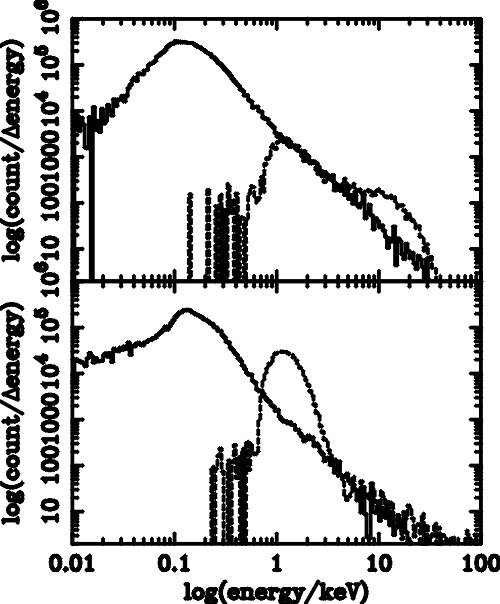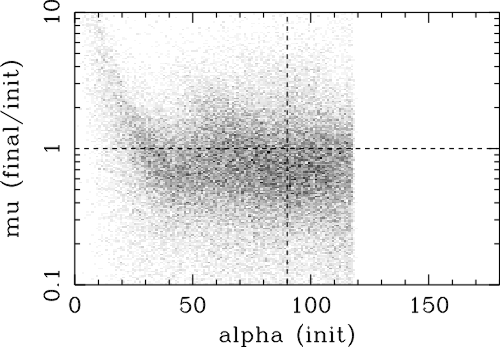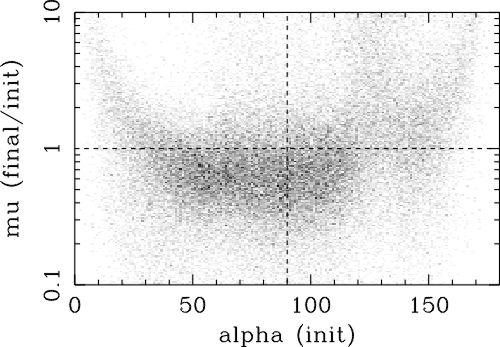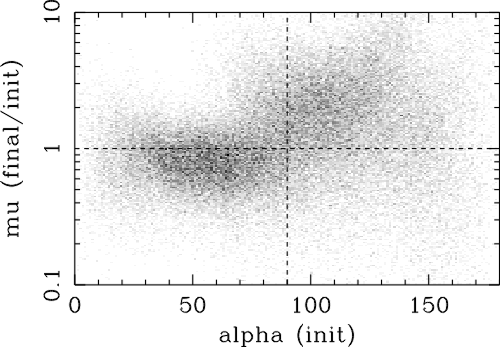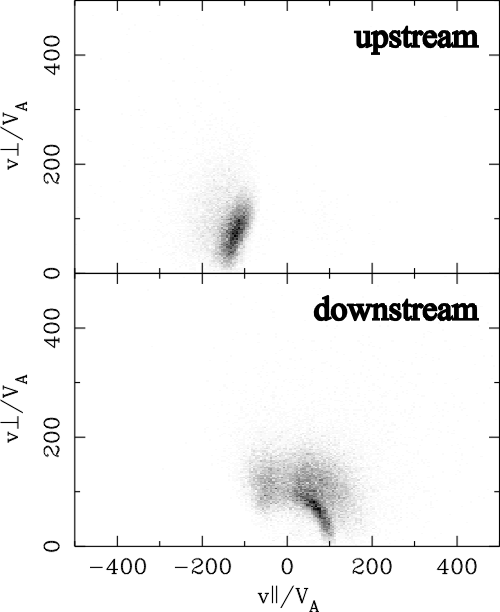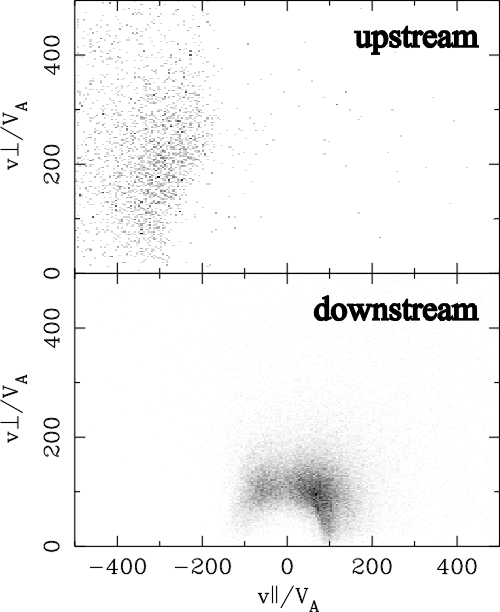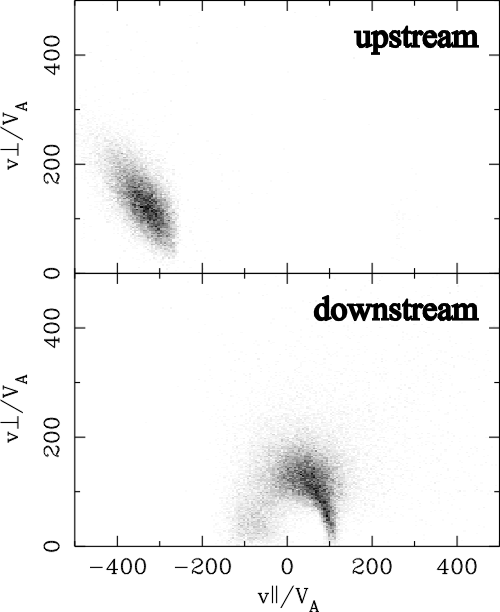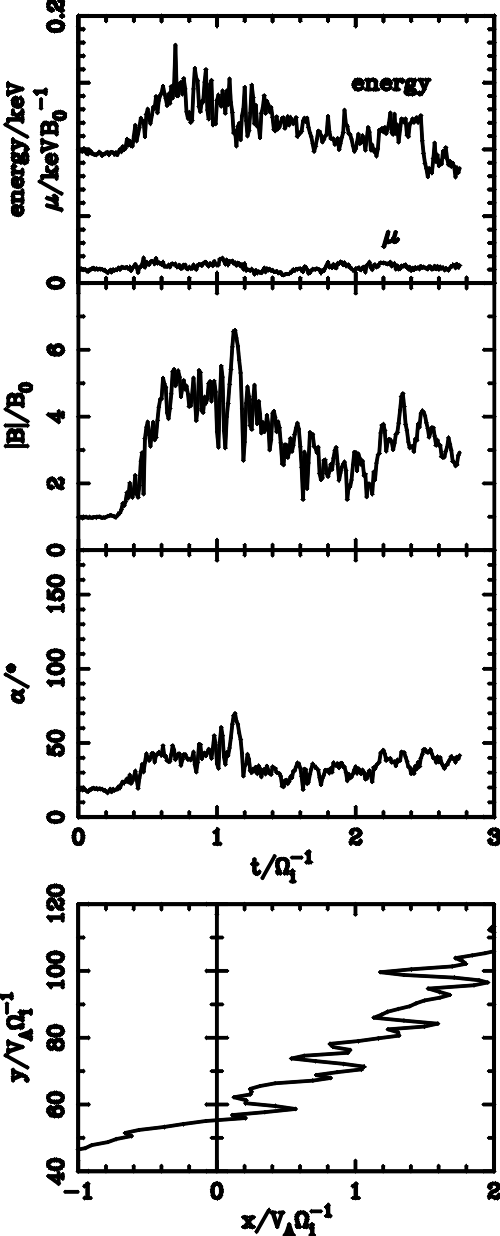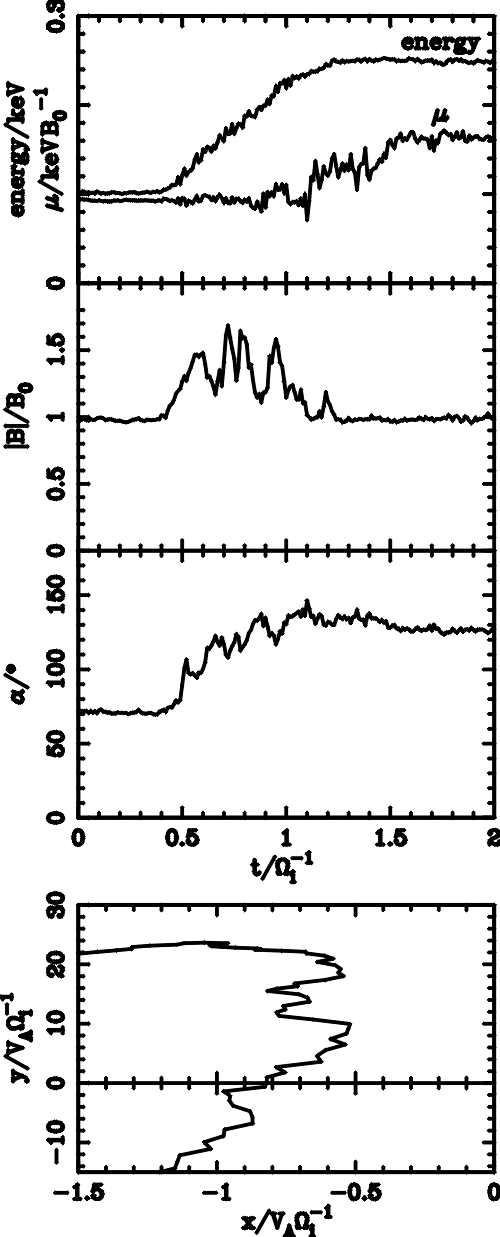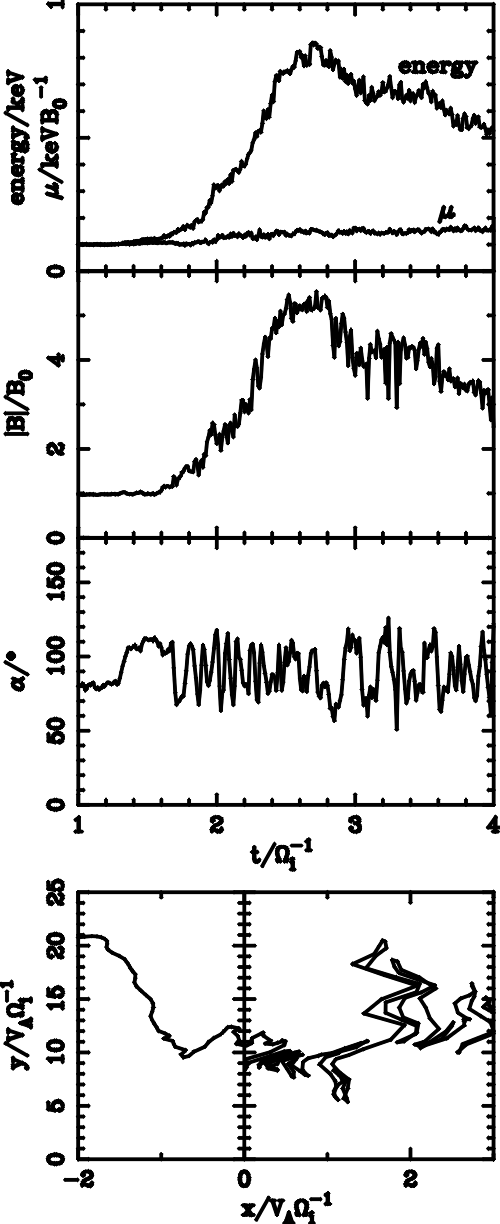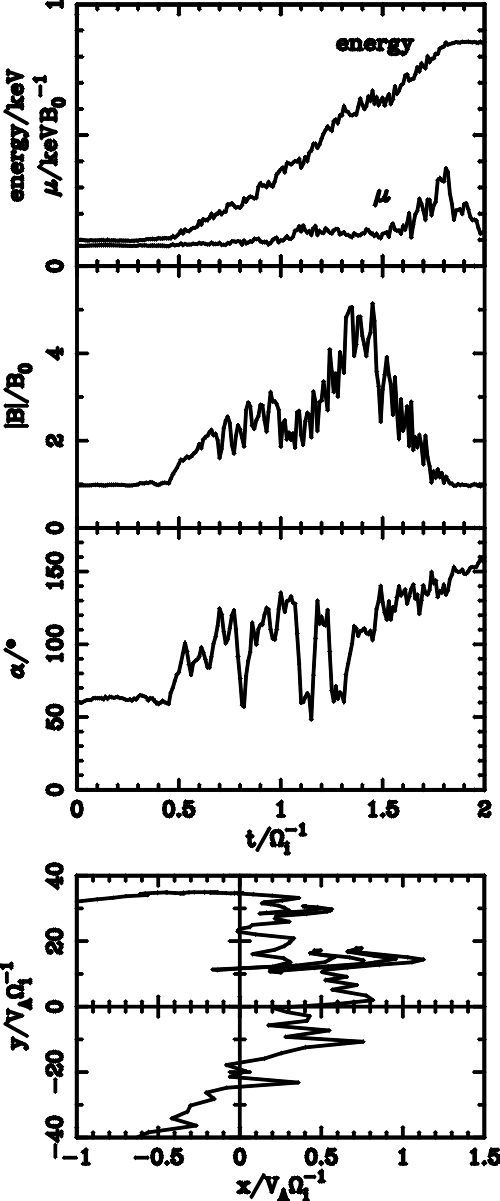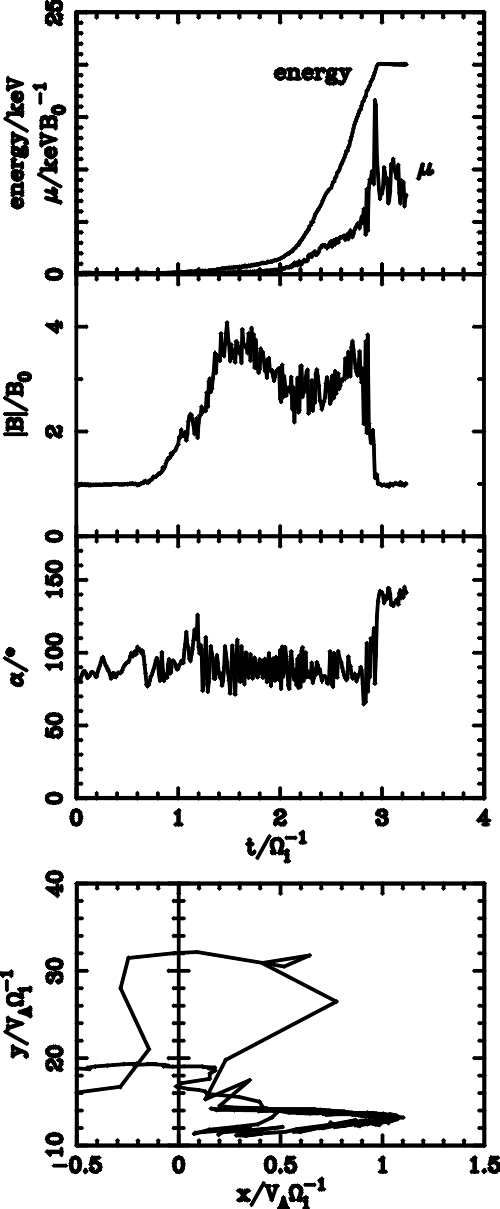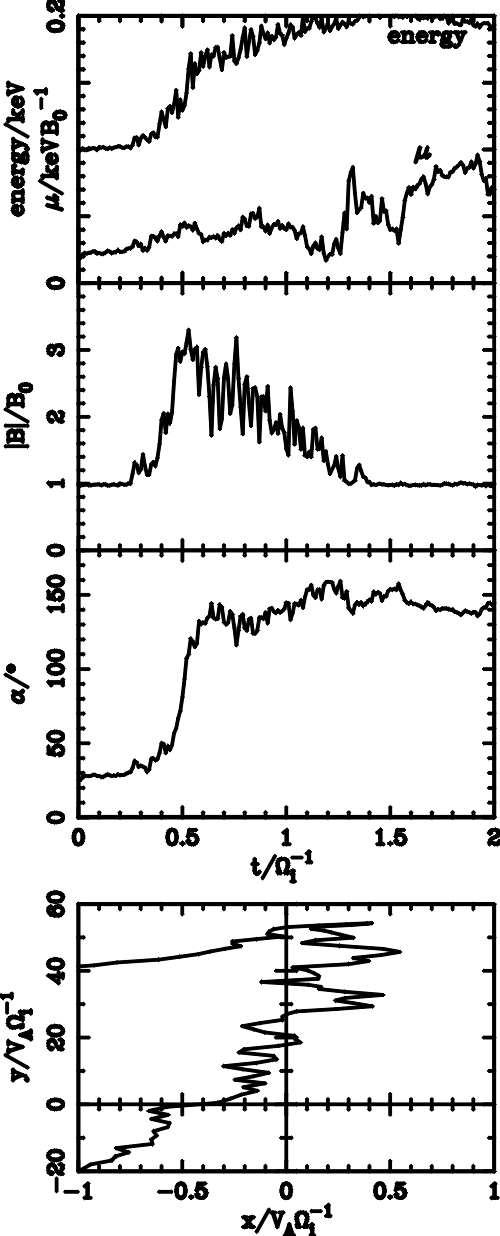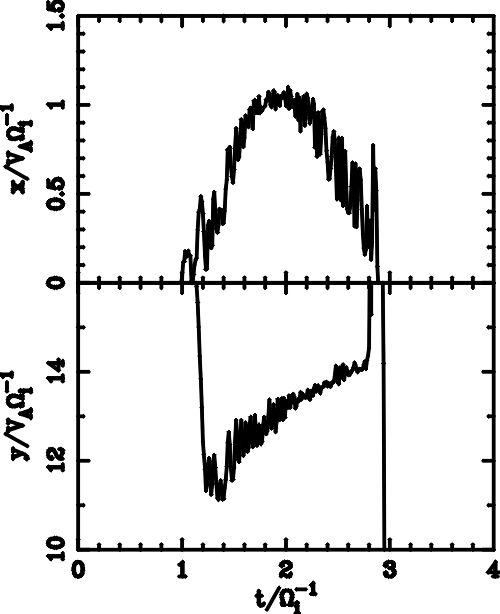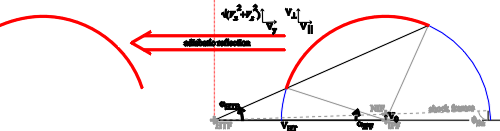
| (5.1) |
| (5.2) |
| (5.3) |
| (5.4) |
| (5.5) |
| (5.6) |
| (5.7) |
| (5.8) |
| (5.9) |
| (5.10) |

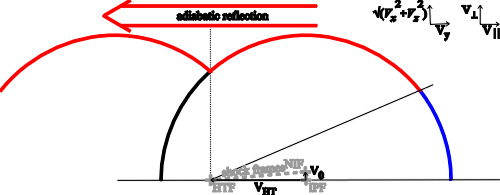
| (5.11) |
| (5.12) |
| (5.13) |
| (5.14) |
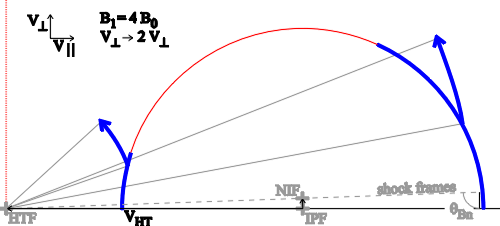
| (5.15) |
| (5.16) |
| (5.17) |
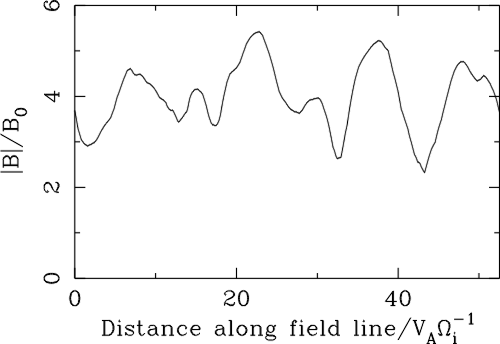
| (5.18) |
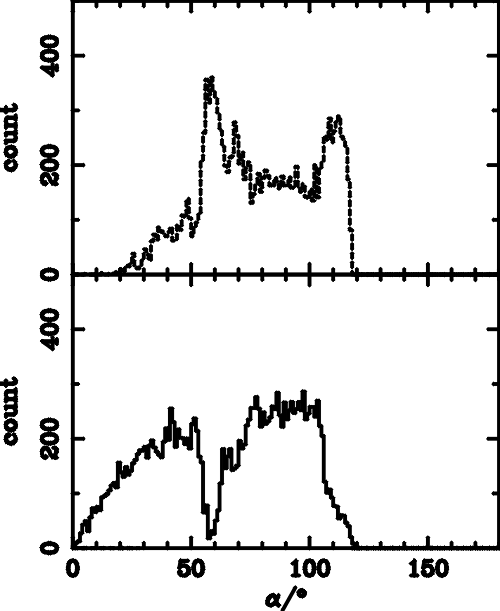
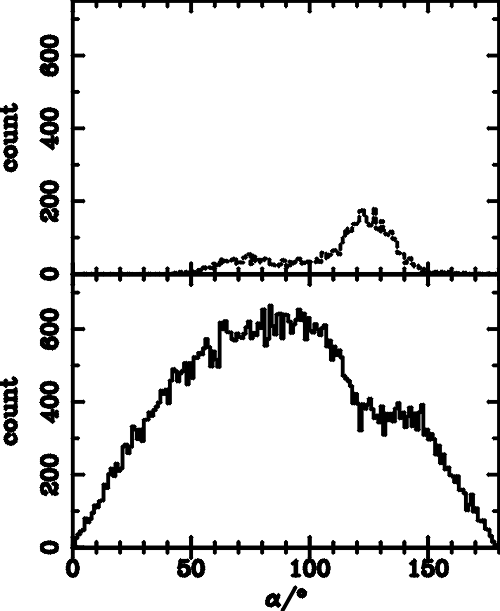
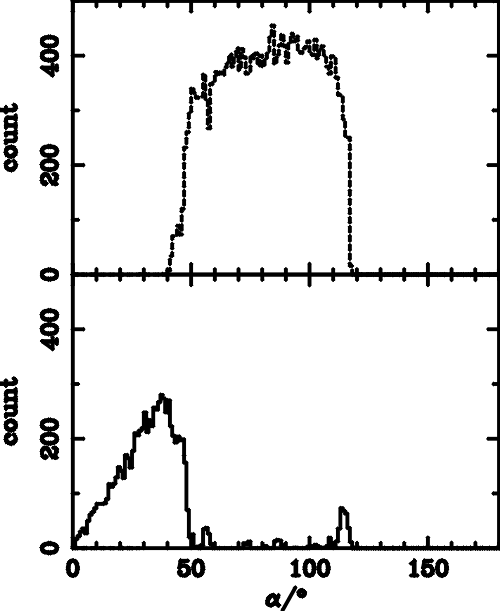
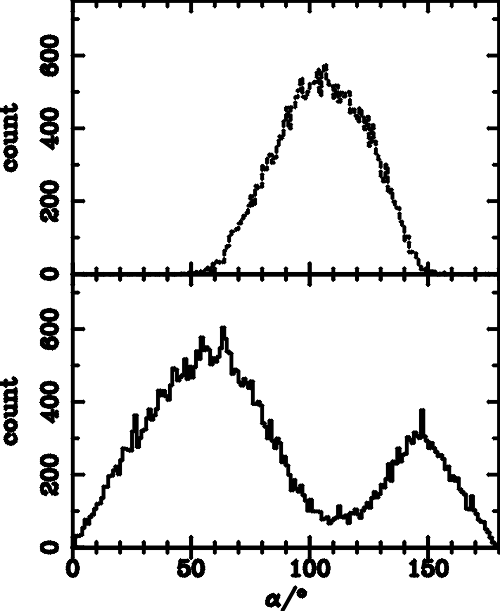
| Parameters | amin | amax | acut-off | Emin | Emax |
| qBn =85� | 55� | 130� | 131� | 100 eV | 420 eV |
| qBn =88� | 88� | 138� | 180� | 690 eV | 1.2 keV |
| Parameters | Upstream | Downstream | In Shock |
| qBn =85�, adiabatic | 74% | 26% | - |
| qBn =85�, B0 out of plane | 73.9% | 23.4% | 2.7% |
| qBn =85�, B0 in plane | 46.8% | 51.7% | 1.5% |
| qBn =88�, adiabatic | 39% | 61% | - |
| qBn =88�, B0 out of plane | 27.2% | 71.6% | 1.2% |
| qBn =88�, B0 in plane | 3.2% | 96.7% | 0.1% |